Tip 1: Jak zjistit výšku čtyřhranného hranolu
Tip 1: Jak zjistit výšku čtyřhranného hranolu
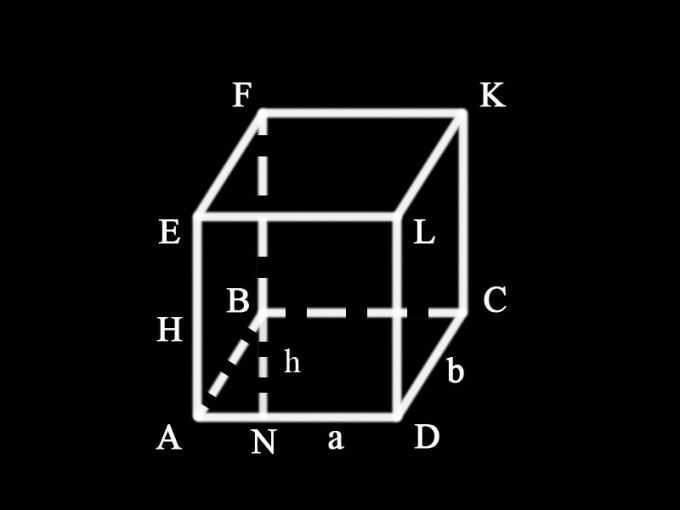
Prism je volumetrická postava složená zřadu obdélníkových bočních ploch a dvou základů rovnoběžných mezi sebou. Základny mohou mít podobu libovolného mnohoúhelníku, včetně čtyřúhelníku. Výška tohoto čísla je segment, kolmý k základům, mezi rovinami, ve kterých leží. Jeho délka v obecném případě je určena úhlem sklonu bočních ploch k základnám hranoly.

Pokyny
1
Pokud v podmínkách problému je objem (V) prostoru ohraničeného obrysy hranoly, a oblast jeho základny (y) pro výpočetvýška (H), použijte vzorec společný pro hranoly se základnou jakéhokoliv geometrického tvaru. Rozdělit hlasitost na základní plochu: H = V / s. Například s objemem 1200 cm³ a základní plochou 150 cm², výška hranoly by měla být rovna 1200/150 = 8 cm.
2
Pokud je čtyřúhelník v základně hranoly, má tvar jakékoli správné postavy, namísto plochy ve výpočtech můžete použít délky okrajů hranoly. Například se čtvercovou základnou oblast vVzorec předchozího kroku nahradit druhý stupeň délky jeho hrany (a): H = V / a². A v případě obdélníku ve stejném vzorci nahraďte produkt délky dvou sousedních okrajů základny (a a b): H = V / (a * b).
3
Pro výpočet výšky (H) pravidelného čtyřúhelníku hranoly Může být dostatečné poznat celou plochupovrch (S) a délka základnové hrany (a). Vzhledem k tomu, že celková plocha čtverců se skládá ze dvou základen a čtyřmi bočními stěnami, a tím, že polyhedron základna je čtverec, jedna boční plocha se musí rovnat (S-a?) / 4. Tato plocha má dvě společné hrany s čtvercovými bází známých velikosti, prostředky pro výpočet délky jiné okrajové oblasti a dělit čtvercovým strany: (S-a?) / (4 * a). Vzhledem k tomu, považována hranol je obdélníkový, délka hrany vypočtená si přilehlé k základně pod úhlem 90 °, tj. To se shoduje s výškou polyhedron: H = (S-a?) / (4 * a).
4
Ve správném čtvercovém hranolu proVýpočet výšky (H) je dostatečný k poznání délky úhlopříčky (L) a jednoho okraje základny (a). Zvažte trojúhelník tvořený touto úhlopříčkou, úhlopříčkou čtvercového základu a jedním z bočních žeber. Hrana je zde neznámou veličinou, která se shoduje s požadovanou výškou, a úhlopříčka náměstí, založená na Pythagorově větu, se rovná výsledku délky strany na kořeně dvou. V souladu se stejnou větou vyjadřte požadovanou hodnotu (cathet) přes délky diagonály hranoly (hypotenze) a úhlopříčky základny (druhá noha): H = √ (L2- (a * V2) ²) = √ (L²-2 * a²).
Tip 2: Jak vytvořit hranol
Prism je zařízení, které sdílí normálnísvětlo na jednotlivých barvách: červená, oranžová, žlutá, zelená, modrá, modrá, fialová. Jedná se o průsvitný objekt s plochým povrchem, který odráží světlé vlny podle jejich délky a díky tomu umožňuje vidět světlo v různých barvách. Make hranol sami poměrně snadno.

Budete potřebovat
- Dva listy papíru
- Fólie
- Sklo
- Kompaktní disk
- Konferenční stolek
- Svítilna
- Pin
- Voda
Pokyny
1
Prism může být vyroben z jednoduchého skla. Naplňte sklenici vodou o něco více než polovinu. Umístěte sklo na okraj konferenčního stolku tak, aby téměř polovina spodní části skla byla zavěšena ve vzduchu. Zároveň ujistěte se, že je sklo na stolu stabilní.
2
Položte dva listy papíru jeden vedle druhého ke konferenčnímu stolu. Zapněte baterku a osvětlete světlo sklem tak, aby padlo na papír.
3
Upravte pozici baterky a papíru, dokud neuvidíte na listu duhu - takže se paprsek světla rozkládá do spektra.
Tip 3: Jak najít okraj čtyřjádrové pyramidy
Čtyřhranná pyramida je pentaedrončtyřhrannou základnou a bočním povrchem čtyř trojúhelníkových ploch. Boční hrany polyhedronu se v jednom bodě protínají - horní část pyramidy.

Pokyny
1
Čtyřhranná pyramida může být správná,obdélníkový nebo libovolný. Pravidelná pyramida má pravidelně čtyřúhelník ve své základně a její vrchol je navržen do středu základny. Vzdálenost od vrcholu pyramidy k její základně se nazývá výška pyramidy. Boční plochy pravidelné pyramidy jsou rovnoramenné trojúhelníky a všechny hrany jsou stejné.
2
Na základně pravidelné čtvercové pyramidymůže ležet čtvercový nebo obdélník. Výška H takové pyramidy je promítnuta do průsečíku diagonálů základny. Na čtverci a obdélníku jsou diagonály d stejné. Všechny boční hrany L pyramidy se čtvercovou nebo obdélníkovou základnou jsou stejné.
3
Chcete-li najít okraj pyramidy, zvažtepravý trojúhelník se stranami: přeponou - požadovaný okraj L, nohy - výška H pyramidy, a polovina úhlopříčky d báze. Vypočítá se okraj o Pythagorovy věty: čtverec přepony je rovna součtu čtverců nohy: L² = H² + (d / 2) ². V jehlanu s kosočtverce nebo paralelogramu v základně protilehlých okrajích jsou stejné a jsou stanoveny podle vzorců: L₁² = H² + (d₁ / 2) ² a L₂² = H² + (d₂ / 2) ², kde d₁ a d₂ - základna diagonální.
4
V pravoúhlé čtverhranné pyramidě jehopředpokládá vrchol jeden z vrcholů v základní rovině dvou ze čtyř bočních stěn jsou kolmo k základní rovině. Jedním z žeber pyramidy se shoduje s výškou H, a dvě boční plochy jsou pravoúhlé trojúhelníky. Vezměme si tyto obdélníkové trojúhelníky: ve kterém jeden z nohou - okraj pyramidy, který se shoduje s jeho výšky H, druhé nohy - základní a straně b a přepona - neznámý pyramida hrany L₁ a L₂. V důsledku toho, že oba okraje pyramidy získat Pythagorovy věty jako pravoúhlé trojúhelníky přepony: L₁² = H² + a? A L₂² = H² + b?.
5
Zbývající čtvrtý okraj LNobdélníkový pyramida získat Pythagorovy věty jako přepony pravoúhlého trojúhelníka s nohama a H d, kde d - báze úhlopříčka čerpaných z okraje základny se shoduje s výškou H pyramidy na spodních okrajích titulní L₃: L₃² = H² + d².
6
V libovolné pyramidě je její vrchol promítánnáhodný bod na dně. Pro zjištění hrany pyramidy uvažovat postupně každý z pravoúhlých trojúhelníků přepona, ve kterém - požadované žebra, jeden z nohy - výška pyramidy, a druhé rameno - úsek spojující vrchol s odpovídajícím základní výšky základny. Pro zjištění hodnoty těchto segmentů musí brát v úvahu trojúhelníky vytvořené v základně v místě připojení na projekčních vrcholů a čtyřstranné pyramidových úhlů.